통계는 사회의 여러 현상을 설명하는 숫자이다. 최근에는 데이터 처리속도와 기술의 발달로 표본이 아닌 전수조사도 가능해졌다고 하지만, 전통적인 통계는 모집단 전체를 대표하는 표본을 추출하여서 특징을 살펴 봄으로써, 모집단의 특징을 이해하는 것이라고 볼 수 있다. 즉, A회사에 근무하는 직원 50,000명을 대상으로 근무 만족도 조사를 한다고 할 때, 전체 설문조사가 어려우니 대표로 1,000명 쯤을 골라내서 설문조사를 한 뒤, 이들의 만족도가 곧 50,000명을 대표하는 것이라고 가정하는 것이다.
물론, 50,000명에 달하는 인원의 전체 조사가 가능하다면, 정확성은 좀 더 높은 수준으로 보장 받겠지만 결코 시간과 비용의 투자가 효율적이지 못할 수 있다. 무엇보다도 그렇게 하는 것이 얼마나 의미가 있냐는 것이다. 1,000명의 직장생활 만족도가 68%인데, 50,000명의 직장생활 만족도가 65%라면 어떨까? 3%의 차이는 모든 시간과 비용 투자를 치를만큼 의미가 있을까에 대한 판단이 필요하다.
알고가기 ㅣ 표본이란?
표본(표할 標, 근본 本)은 어떤 것의 본보기가 되거나 표준을 삼을만한 것이다. 통계에서는 모집단을 대표하는 집단으로 통계분석의 대상이 되는 집단을 의미한다. 본보기로 표본은 example을 주로 사용하고, 통계에서 표본은 sample로 생각하면 이해가 쉽다.
주의할 점은, 어떤 표본을 고르느냐에 따라서 결과를 임의로 조작하거나 왜곡할 수 있기 때문에 표본을 골라내는 방법이 매우 중요하다. 예를 들어서, 대통령 선거 전에 국민들의 의견을 들어보는 여론조사에서 특정 지역에만 조사를 집중한다면 전체 결과를 반영할 수 있을까? 그렇지 않다. 우리는 기본적으로 지역에 따라하서 선호하는 정당이 어느정도 다름을 알고 있으므로, 특정 지역에서만 여론조사한 결과를 전체의 결과라고 공개하면 반드시 반발할 것이다.
자, 표본을 잘 추출해야 한다는 것은 알겠다. 그렇다면 통계 표본을 추출하는 방법에는 어떤 것들이 있을지 알아보겠다. 크게 네 가지로, 단순랜덤추출법, 계통추출법, 집락추출법, 층화추출법이 있다. 평소에 쓰는 단어가 달라서 쉽게 의미가 상상은 되지 않는다. 하나 씩 짚어보겠다.
단순랜덤 추출법(Simple random sampling)
이름 값을 하는 방법이다. 단순하게 랜덤으로 추출한다는 의미이고, 모든 샘플이 선택될 확률이 동일하다. 복원추출방법과 비복원 추출방법이 있는데, 복원추출방법은 한 번 뽑은 샘플을 다음 선택에 또 포함하는 것이고, 비복원 추출방법은 한 번 선택되었으면 그 다음 선택에서 제외되는 것이다. 우리에게 친숙한 로또 추첨방법은 비복원 추출방법이다. 1번부터 45번까지 6개의 숫자를 선택하는데, 첫 번째로 2번 공을 뽑았다면, 2번 공은 다시 뽑기에 포함되지 않으며, 최종 6개의 숫자는 모두 다른 숫자가 된다.
계통추출법(Systematic sampling)
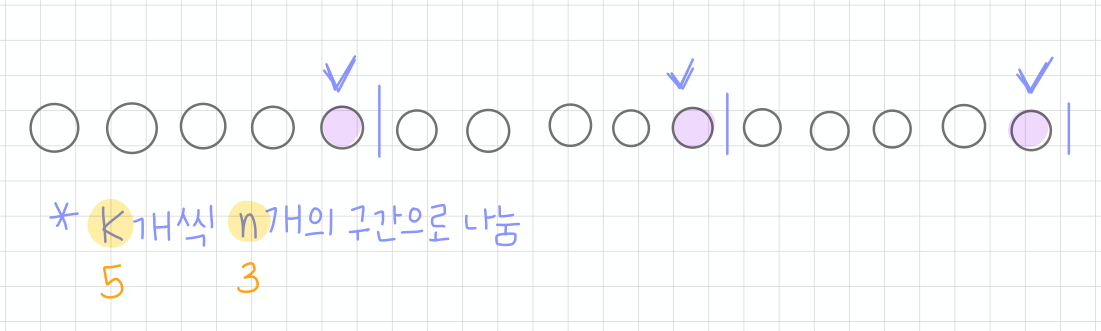
단순랜덤추출법을 변형시킨 방식이다. 전체 샘플을 나열한 뒤에, K개씩 n개의 구간으로 나눈다. 예를 들면, 전체 15개의 샘플이 있다면, 5개씩(K) 3등분(n)을 하면, 아래 그림처럼 표현할 수 있다. 매번 K번째 샘플을 선택하는 방법이다. K개씩 계통을 나눈다고 생각하고 명칭과 매칭시키면 되겠다.
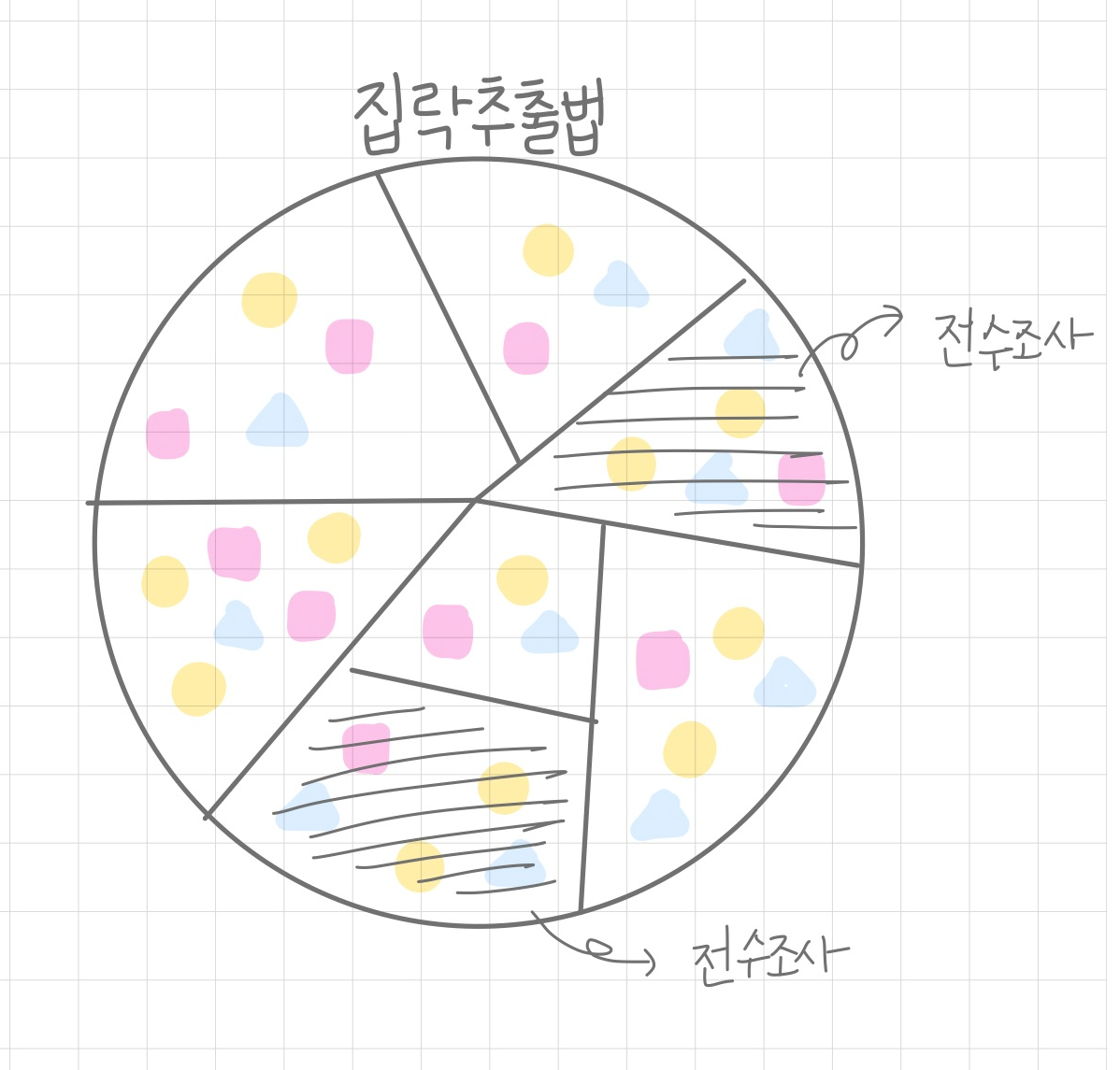
집락추출법(Cluster random sampling)
집락은 무리를 의미한다. 전체 모집단에서 무리를 지어서 나누어본다는 것이다. 지역표본추출처럼 무리 구분이 명확할 때, 무리를 나누어서 무리 안에서 랜덤 추출을 진행하는 것이다. 예를 들어서, A중학교 3학년 학생들을 조사한다고 할 때, 1반부터 10반까지 전체를 조사하지 않고, 2반과 8반만 조사하는 것이다.
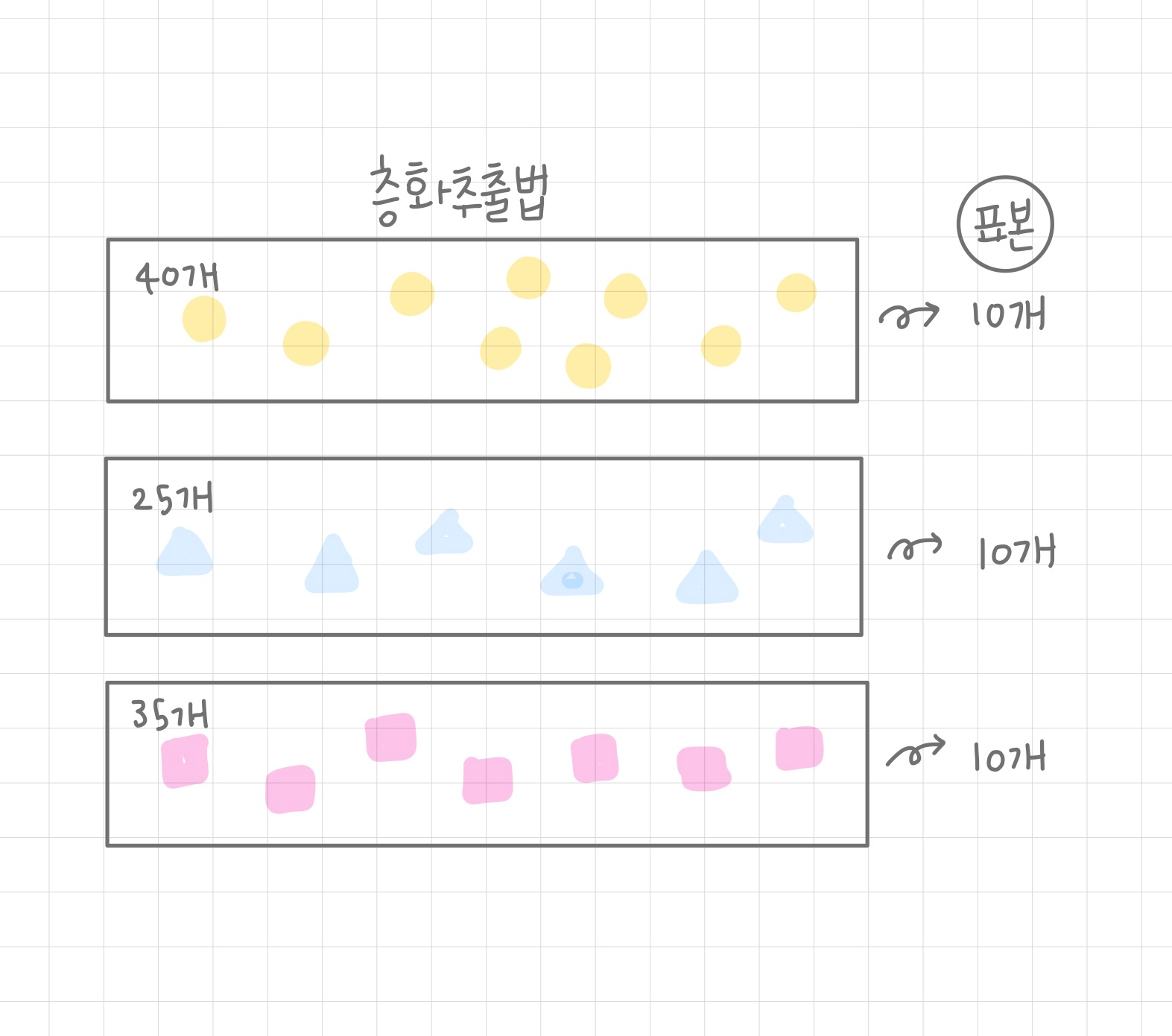
층화추출법(Stratified random sampling)
층화추출법은 각 샘플의 특징이 같은 것들로 묶어서 층을 나눈 다음에, 각 층에서 샘플을 추출한다. 같은 것으로 묶는 절차가 있기 때문에 집단 내에서 샘플들은 성질이 동일하고, 각 집단 간에는 서로 다른 특징을 갖는다. 예를 들어서, 연령대별로 조사하는 경우, 각 연령대를 층으로 나누고, 각 연령대에서 n개의 샘플을 추출하는 방법이 되겠다. 각 층들은 이질적인 특징을 갖는 경우에 해당하는 추출법이다.
집락추출법과 층화추출법의 차이
여기까지 읽으면, 집락추출법과 층화추출법을 이해하는데 다소 혼동이 생길 수 있다. 확실하게 이해하고 넘어가보자.
집락추출법은 무리가 나누어져 있고, 각 무리가 이미 전체 모집단을 대표할 수 있어야 한다.
층화추출법은 비슷한 성질을 같은 층을 따로따로 나눈 다음에 각 샘플을 골라내어서, 표본이 모집단의 구성원을 잘 대변할 수 있도록 하는 것이다. 연령대가 다양하게 구성되어 있는 모집단에서, 단순하게 랜덤으로만 추출하면 10대가 80%, 30대 10%, 60대가 10% 형태로 비율이 맞지 않을 수가 있다. 비율 문제를 고려할 땐, 층화추출법을 기억하자!
응용 문제를 맞춰보자.
서울시에서 코로나 정부지원금이 지급된 2021년 9월에 자영업자들의 전월대비 매출 증가량을 조사한다고 해보자. 전수조사를 하기엔 효율적이지 않으니 정부지원금이 적용되는 대상 업체와, 지원이 되지 않는 업체를 나누어서 비교해보고자 한다면 어떤 추출법이 더 적당할까?
층화추출법에 가깝다고 볼 수 있겠다. 정부지원금이 적용되는 대상업체와 그렇지 않은 업체는 '지원금 대상 여부'에 관해서 이질성을 갖기 때문에 층을 따로 나누어서 비율을 맞추어야 할 것이다. 만일 무작위로 추출해서 지원금 대상이 아닌 업체가 표본의 80%를 이룬다면 정부지원금은 전혀 효과가 실제보다 낮게 보여질 수 있다. 집락으로 하기엔 두 집단이 이질성을 갖기 때문에 전제조건 부터가 맞지 않다.
단순사례 보다는 실질적인 예를 통해서 실생활에서 표본추출을 가까이서 찾아보았다.
'All about Data > Statistics' 카테고리의 다른 글
| 한국 무역, 수출입 통계를 품목별로 조회하는 방법 (0) | 2024.07.12 |
|---|---|
| 지니계수와 로렌츠 곡선의 개념과 공식, 쉽게 이해하기 (0) | 2021.09.24 |
| 1/n이 평균의 전부가 아니다, 산술평균+기하평균+조화평균의 공식과 예시 (1) | 2021.09.24 |
| F1 Score, Roc곡선, Auc 계산방법 / scikit-learn 코드로 구현하기 (0) | 2021.09.16 |
| 정밀도(precision)와 재현율(recall) 오차행렬 안 헷갈리는 방법, 분류모델 평가지표 (3) | 2021.09.15 |



